Connections
Spring-Summer 2016
Photo Contest
The Center for International Education sponsors an annual student photo competition. READ »
Special Agent James Cheeks, FBI
James Cheeks '95 busts drug dealers and corrupt cops, all in a day’s work. READ »
Math Revolution
What if everyone changed the way they taught math? One Nazareth professor is at the forefront of a growing national movement. READ »
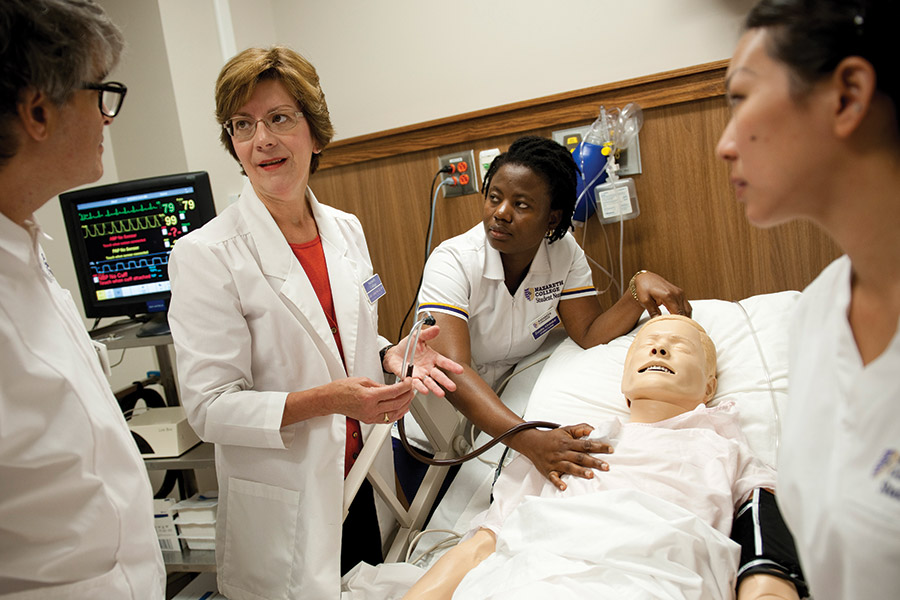
Rx for Nursing
New, state-of-the-art facilities and a more rigorous curriculum have revitalized the long-standing program. READ »
Small Molecule, Big Discovery
Hydrofracking has created an ecological problem. Stephen Tajc, Ph.D., may have the solution. READ »
9 Questions
John J. Drain ’83 is the senior vice president, finance, of Hearst Television, Inc. READ »
Can-Do Attitude
Sofiya Kreminska ’16 makes the most of Nazareth’s experiential learning opportunities. READ »